Building a Neural Network in Rust (From Scratch)
Read on dev.to
Let’s build a neural network from scratch to truly understand how they work. And by scratch, I mean without using any fancy ML or linear algebra libraries. We’re going to build a single-layer perceptron, the simplest neural network there is, and then teach it to perform addition.
I’ll be using Rust but you can follow along using the JavaScript or Python implementations if that’s what you prefer. Code is available here.
Neural Network
A neural network is exactly what it sounds like; A network of artificial neurons. A neuron or “node” is a computational unit that mimics the function of a biological neuron. It receives some input, performs some math on it, and then spits out an output.
We’ll start by defining a NeuralNetwork struct and an associated method to initialize it. We don’t have much to go on yet so let’s leave it empty for now.
struct NeuralNetwork {}
impl NeuralNetwork {
fn new() -> Self {
Self {}
}
}
Layers
Neurons in a neural network are grouped into levels called layers. Each layer processes the input in some way and each layer’s output serves as input to the next layer. The first layer receives the initial input, and the last layer produces the final output. Layers in between are called hidden layers and help in extracting and transforming features from the data.
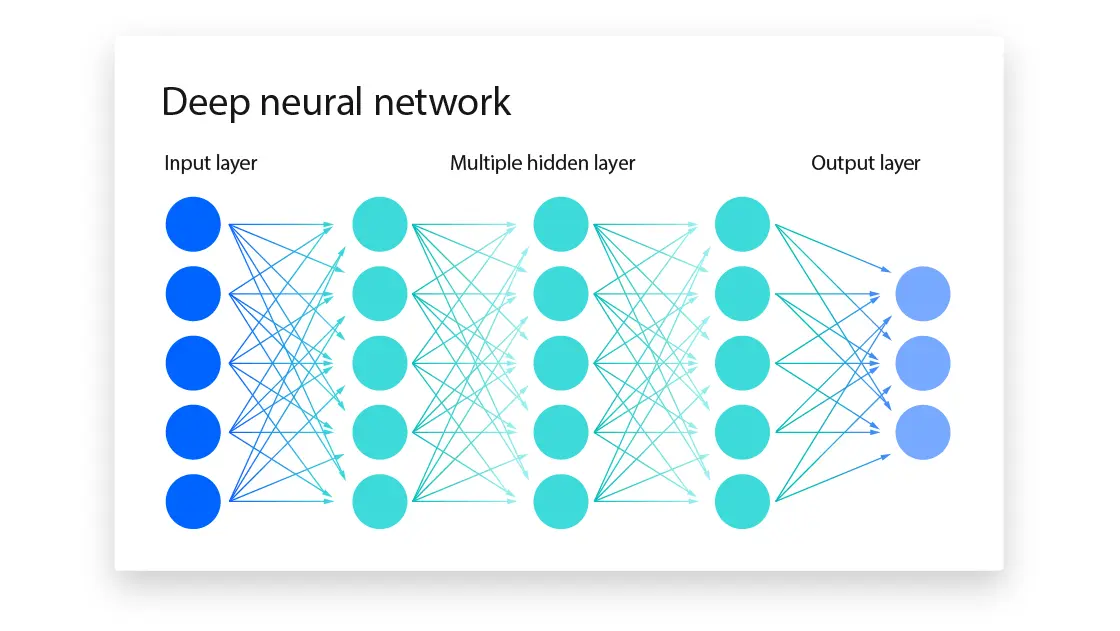
Each circle represents a neuron and each line, a connection. You can see that each neuron in a layer is connected to every neuron in the next layer.
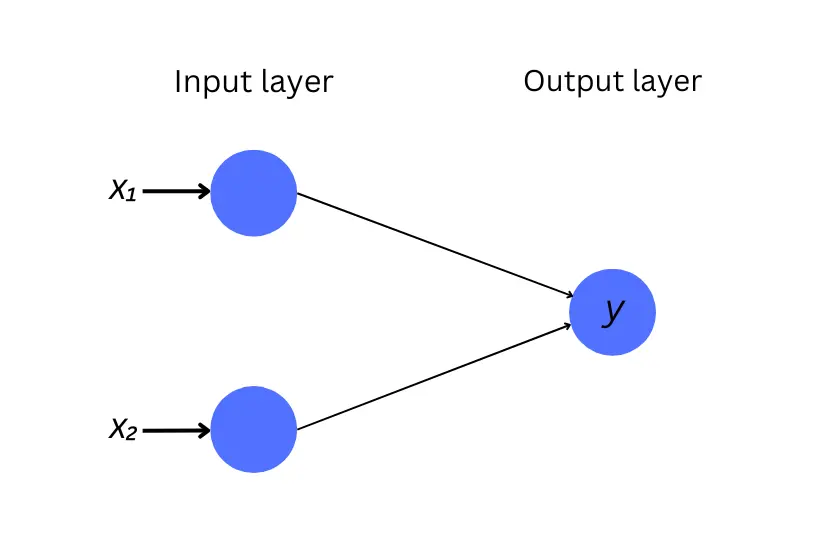
The neural network we’re building looks like this. It has two input neurons (one for each number) and an output neuron. Note that it doesn’t have any hidden layers.
Weights
Each connection in a neural network has an associated weight. These weights determine the strength and direction (positive or negative influence) of the relationship between neurons, which in turn influences how the data is transformed as it passes from one layer to the next. During the training process, we adjust these weight values to reduce the error in the output.
A good way of thinking about weights is to imagine the neural connections as tubes which carry the signals (data) from one neuron to the next. These tubes can change thickness. A thicker tube means the connection it represents is stronger, influencing the signal that passes through it more significantly.
Since there are no hidden layers in our network, we only need two weights (one for each connection). We’ll initialize them to random floating point values for now.
struct NeuralNetwork {
weights: Vec<f64>
}
impl NeuralNetwork {
fn new() -> Self {
let mut rng = rand::thread_rng();
let weights = vec![rng.gen_range(0.0..1.0), rng.gen_range(0.0..1.0)];
Self {
weights
}
}
}
Bias
Bias is another parameter that adjusts the output of a neuron. Imagine a small knob alongside each neuron. This knob can adjust how active the neuron is, regardless of the signals it receives. It’s like tweaking the baseline level of activity for the neuron, ensuring that even if all incoming signals are weak, the neuron can still choose to fire (activate) based on this bias adjustment.
Only the neurons in the hidden and output layers have a bias. Since our perceptron has no hidden layers and only a single neuron in the output layer, we only need a single bias value which we’ll also initialize to a random value.
struct NeuralNetwork {
// [...]
bias: f64
}
impl NeuralNetwork {
fn new() -> Self {
// [...]
Self {
// [...]
bias: rng.gen_range(0.0..1.0)
}
}
}
Activation Function
The activation function is what decides whether a neuron should fire or not. It’s like a filter or a gatekeeper of sorts that looks at the incoming signals (after being modified by weights and bias) and decides how brightly the neuron should light up. Activation functions are used to introduce non-linearity in the network. This non-linearity allows the network to learn complex patterns.
The output of a neuron can be computed as:
We multiply the outgoing connection’s weight by the input, add the bias and apply the activation function on the result.
impl NeuralNetwork {
// [...]
fn predict(&self, input: &[f64; 2]) -> f64 {
let mut sum = self.bias;
for (i, weight) in self.weights.iter().enumerate() {
sum += input[i] * weight;
}
sigmoid(sum)
}
}
Sigmoid is a relatively simple non-linear activation function. All it does is transform its argument into a value between 0 and 1, though not linearly. Try calling it with different values to see how it works.
fn sigmoid(x: f64) -> f64 {
1.0 / (1.0 + (-x).exp())
}
Backpropagation
This is the key algorithm for training neural networks. If the final output isn’t what we expect, we “propagate” the error “backwards” through the layers of the network and find out which paths (connections) contributed how much to the overall error in the final output. We then use this information to slightly adjust the weights and biases in the network in a way that will reduce the error in future outputs. We repeat this process again and again, gradually optimizing the network’s parameters until its output is close enough to what we expect.
impl NeuralNetwork {
// [...]
fn train(&mut self, inputs: Vec<[f64; 2]>, outputs: Vec<f64>, epochs: usize) {
for _ in 0..epochs {
for (i, input) in inputs.iter().enumerate() {
// Get a prediction for a given input
let output = self.predict(input);
// Compute the difference between the actual and the desired output
let error = outputs[i] - output;
// Find the gradient of the loss function
// (sort of like a hint about the direction to adjust the weights in)
let delta = derivative(output);
// Adjust the weights and the bias to reduce error in the output
for j in 0..self.weights.len() {
self.weights[j] += self.learning_rate * error * input[j] * delta;
}
self.bias += self.learning_rate * error * delta;
}
}
}
}
fn derivative(x: f64) -> f64 {
x * (1.0 - x)
}
An epoch is one complete pass through the entire training dataset. In every epoch, we feed each set of inputs in the training data to our network, compare its output to what it should be and use the difference to readjust its parameters. We repeat this process for multiple epochs to refine the model’s performance.
One last step is to add the learning rate to our network. It’s a constant value that determines how quickly the model learns from its mistakes. We’ll set it to 0.1.
struct NeuralNetwork {
// [...]
learning_rate: f64,
}
impl NeuralNetwork {
fn new() -> Self {
// [...]
Self {
// [...]
learning_rate: 0.1,
}
}
Now that our neural network is ready, let’s use it.
fn main() {
let d = data::get_data().unwrap();
let inputs = d.training_inputs;
let outputs = d.training_outputs;
let test_inputs = d.test_inputs;
// Initialize the network
let mut neural_net = NeuralNetwork::new();
for input in test_inputs.iter() {
// Pass a set of inputs (two numbers) and get a prediction back which should be the sum of the two numbers
let prediction = neural_net.predict(input);
println!("Input: {:?}, Prediction: {:.1}", input, prediction);
}
}
If you run it, you’ll get some output that looks like this.
Input: [0.9, 0.1], Prediction: 0.7
Input: [0.5, 0.5], Prediction: 0.7
Input: [0.2, 0.3], Prediction: 0.7
Input: [0.3, 0.6], Prediction: 0.7
Input: [0.1, 0.7], Prediction: 0.7
Input: [0.3, 0.1], Prediction: 0.7
Input: [0.1, 0.5], Prediction: 0.7
Input: [0.9, 0.0], Prediction: 0.7
Input: [0.3, 0.3], Prediction: 0.7
Input: [0.0, 0.1], Prediction: 0.6
Input: [0.1, 0.2], Prediction: 0.7
Input: [0.2, 0.0], Prediction: 0.6
Input: [0.6, 0.1], Prediction: 0.7
Input: [0.5, 0.3], Prediction: 0.7
Input: [0.9, 0.1], Prediction: 0.7
Input: [0.1, 0.4], Prediction: 0.7
Input: [0.2, 0.4], Prediction: 0.7
Input: [0.7, 0.0], Prediction: 0.7
Input: [0.6, 0.3], Prediction: 0.7
Input: [0.2, 0.2], Prediction: 0.7
Input: [0.1, 0.0], Prediction: 0.6
Input: [0.2, 0.6], Prediction: 0.7
Input: [0.5, 0.0], Prediction: 0.7
Input: [0.6, 0.4], Prediction: 0.7
Input: [0.4, 0.5], Prediction: 0.7
We can see that our network is very bad at its job of adding numbers. It only gets 2 out of 25 predictions right and that too out of sheer chance. This is because we haven’t trained it yet. Let’s add the training step.
let mut neural_net = NeuralNetwork::new();
// Train for 10000 epochs
neural_net.train(inputs, outputs, 10000);
Run it again and…
Input: [0.9, 0.1], Prediction: 0.9
Input: [0.5, 0.5], Prediction: 0.9
Input: [0.2, 0.3], Prediction: 0.5
Input: [0.3, 0.6], Prediction: 0.9
Input: [0.1, 0.7], Prediction: 0.8
Input: [0.3, 0.1], Prediction: 0.4
Input: [0.1, 0.5], Prediction: 0.6
Input: [0.9, 0.0], Prediction: 0.9
Input: [0.3, 0.3], Prediction: 0.6
Input: [0.0, 0.1], Prediction: 0.1
Input: [0.1, 0.2], Prediction: 0.3
Input: [0.2, 0.0], Prediction: 0.2
Input: [0.6, 0.1], Prediction: 0.7
Input: [0.5, 0.3], Prediction: 0.8
Input: [0.9, 0.1], Prediction: 0.9
Input: [0.1, 0.4], Prediction: 0.5
Input: [0.2, 0.4], Prediction: 0.6
Input: [0.7, 0.0], Prediction: 0.7
Input: [0.6, 0.3], Prediction: 0.9
Input: [0.2, 0.2], Prediction: 0.4
Input: [0.1, 0.0], Prediction: 0.1
Input: [0.2, 0.6], Prediction: 0.8
Input: [0.5, 0.0], Prediction: 0.5
Input: [0.6, 0.4], Prediction: 0.9
Input: [0.4, 0.5], Prediction: 0.9
Whoa! It correctly guesses the answer around 80% of the time. Not bad.
Our model works because the problem we were trying to solve was extremely simple. Larger neural networks able to “remember” more complex patterns can have hundreds of thousands of neurons across numerous layers along with sophisticated architectures such as convolutional or recurrent neural networks. For instance, GPT-3 is said to have 175 billion parameters while its successor GPT-4 has 1.76 trillion. Compare that to our model which only has 3 parameters (2 weights + 1 bias).
So there you have it. A neural network from scratch, in Rust.